







Worum es in diesem Beitrag geht
Es geht auf Bundesländerebene um mögliche Zusammenhänge der Covid-Todeszahlen mit der Altersstruktur, den Temperaturen und den Impfquoten. Darüber hinaus geht es auch um mögliche Zusammenhänge zwischen Impfquoten und allgemeiner Sterblichkeit. (Hier zunächst aber nur auf bundesdeutscher Ebene.) Außerdem geht es – sehr vereinfacht – um das Thema, was Statistik leisten kann und was nicht und um den Begriff der ″Scheinkorrelationen“.
Einleitung
Seit zwei Jahren muss ich ertragen, wie alle möglichen Zusammenhänge im Hinblick auf Corona ″ermittelt“ und welche Annahmen ″belegt“ seien. Auffällig ist, dass, sobald diese Annahmen dem gewünschten allgemeinen Narrativ entsprechen, sie ohne weiteres Hinterfragen durchgewinkt werden. Aber wehe dem, es kommen Ergebnisse heraus, die diesem Narrativ widersprechen. Ja, dann schafft man es plötzlich und vollkommen wider Erwarten, sich wieder auf statistische Gepflogenheiten zu besinnen und das ganze statistische Waffenarsenal aus dem mittlerweile verstaubten Keller zu holen!
Letztlich zeigt sich vor allem diese übergeordnete ″Korrelation“:
Zusammenhänge sind ″zulässig“, sofern sie die positive Wirkung der Impfung aufzuzeigen scheinen. Wirkliche Belege sind dann auch gar nicht mehr so wichtig. Ist es aber anders, … dann wird schnell die besagte Kellertür aufgerissen und das ganze statistische Arsenal herausgezerrt, um die Häresie schnell und nachhaltig zu unterbinden.
Im Juli 2020 untersuchte ich international (für bis zu 174 Länder) mögliche Zusammenhänge zwischen der Corona-Pandemie (anhand des Indikators der Covid-Toten) und anzunehmenden und plausiblen Faktoren, die einen Einfluss auf den Verlauf der Pandemie bzw. die Höhe der Todesfälle haben könnten. (Quelle: https://coronakrise-blog.jimdofree.com/start/07-07-20-keine-korrelation-zwischen-lockdown-und-covid/)
In diesem Zusammenhang musste ich feststellen, dass eine Korrelation zwischen der Zahl der Covid-Toten und den staatlichen Maßnahmen (Lockdowns etc.) nicht festzustellen war. Allerdings waren andere Zusammenhänge auffällig. Zu diesen gehörten die Altersstruktur einer Gesellschaft, bestimmte Krankheiten wie Demenz oder Diabetes, die Quote der Grippeimpfungen als auch die Durchschnittstemperaturen im relevanten Zeitraum (obwohl bis dahin ein saisonaler Einfluss meist vehement bestritten wurde).
Mittlerweile sind einige dieser Faktoren allgemein anerkannt, finden in der allgemeinen Erzählung aber nicht die ihnen gebührende Gewichtung.
Im Hinblick auf die Covid-Todeszahlen in deutschen Bundesländern will ich nun speziell mögliche Zusammenhänge mit dem Anteil alter Menschen und/oder den Durchschnittstemperaturen genauer betrachten. Ebenso sollen Zusammenhänge zwischen Impfquoten und Covid-Todesfällen aber auch allgemeinen Sterblichkeiten (auf nationaler Ebene) betrachtet werden.
Quellen und Limitierungen der Darstellungen in diesem Beitrag
Herangezogen wurden die Daten vom Bundesamt für Statistik (Destatis), vom Robert-Koch-Institut (RKI) und vom Deutschen Wetterdienst (DWD).
Die konkreten Quellen sind am Ende dieses Beitrages aufgeführt.
Für das Jahr 2021 liegen noch keine abschließenden Bevölkerungszahlen nach Altersgruppen pro Bundesland vor. Destatis hat aber Ende September 2021 Hochrechnungen (unter Berücksichtigung des Einflusses von Corona) unter verschiedenen Prämissen vorgenommen (Quelle: https://www.destatis.de/DE/Themen/Gesellschaft-Umwelt/Bevoelkerung/Bevoelkerungsvorausberechnung/Publikationen/Downloads-Vorausberechnung/bevoelkerung-deutschland-2035-5124202219004.html). Die Minimal- und Maximal-Hochrechnungen unterscheiden sich aber nicht wesentlich voneinander. In diesem Beitrag wurde das Modell mit der etwas geringeren Gesamtbevölkerung verwendet. Das Modell mit der etwas höheren Gesamtbevölkerung würde aber nicht zu signifikant anderen Ergebnissen führen.
Alle Daten sind auf die jeweilge Bevölkerungszahl normiert. Eine Ausnahme ist die Darstellung des Verlaufs der Covid-Toten in Deutschland. Dort wurden Absolutzahlen verwendet.
Zu Korrelationen im Allgemeinen:
Korrelationen machen keine Aussagen zu Ursache und Wirkung.
Die Gefahr von sogenannten Scheinkorrelationen (oder ″spurious correlations“) ist generell gegeben. Es kann kaum ausgeschlossen werden, dass die Korrelation von zwei untersuchten Variablen nicht in Wirklichkeit von einer oder mehreren anderen (und möglicherweise nicht bekannten) Variablen abhängt und damit scheinbare Zusammenhänge aufgezeigt werden, die in Wirklichkeit direkt so nicht bestehen.
Insofern ist trotz statistischer Methoden (so ausgefeilt sie auch sein mögen) immer Folgendes zur Beurteilung wichtig:
- Gesunder Menschenverstand.
- Die grundsätzliche Plausibilität der Hypothesen.
- Die Erkenntnis, dass man alles ″beweisen“ kann, was man nur will, wenn man sich nur genug Mühe gibt und die Daten so aufbereitet, dass sie letztlich das ausspucken, was man sich als Ergebnis wünscht.
- Der Wille oder die vorgefasste Meinung des Untersuchers beeinflusst immer die Art des Vorgehens oder die gewählte Methodik. Keine noch so komplexe Formel verhindert das, sie kann es höchstens verschleiern. Das gilt auch für mich! Ich kann nur garantieren, mir die größte Mühe zu geben, die Daten so objektiv wie möglich aufzubereiten. Aber ich kann nicht oberhalb meines Geistes stehen und ihn von dort aus objektiv betrachten und lenken. Niemand kann das.
- Es gibt keine absoluten Wahrheiten, die man statistisch im eigentlichen Sinne ″beweisen“ könnte. Es gibt nur Näherungen. Statistik kann eine große Hilfe sein, häufig aber auch nicht mehr als das.
Im diesem Beitrag hätte ich zu allen Darstellungen berechnen müssen, wie siginifikant die kalkulierten Korrelationen sind. Das habe ich nicht vorgenommen, weil Aufwand und Nutzen zu diesem Zeitpunkt nicht in einem akzeptablen Verhältnis stehen und weil es insgesamt zu viele Betrachtungen sind, von denen ich hier nur ausgewählte darstelle. Dies kann aber jederzeit von jedem Interessierten nachgeholt werden. Die herangezogenen Daten sind öffentlich verfügbar.
In den in diesem Beitrag dargestellten Grafiken sind die Daten in der Regel normalisiert. Das bedeutet, dass die Rohdaten, welche vollkommen unterschiedliche Skalierungen haben können, jeweils auf eine Skala von 0 bis 1 skaliert wurden. Das ändert nichts an den Korrelationen oder am Aussehen der Grafiken. Der Grund dafür ist aber Folgender: Es können mehrere unabhängige Variablen gemeinsam einen Einfluss auf eine abhängige Variable haben (hier in der Regel die Covid-Toten). Um diese unabhängigen (oder bestimmenden) Variablen zusammenfassen (addieren) zu können, müssen sie auf eine gemeinsame Skala umgerechnet werden.
Um ein Beispiel zu nennen: Ich kann zwar durchaus in einem Bundesland einen Anteil über 80-Jähriger von 6,25 % und eine Covid-Todeszahl von 49,94 pro 100 Tausend in Beziehung setzen. Aber ich kann es dann nicht mehr, wenn ich noch eine weitere Variable hinzuziehe, wie zum Beispiel eine Durchschnittstemperatur von -0,70 Grad Celsius.
Um mehrere Variablen mit unterschiedlichen Skalierungen miteinander in Beziehung zu setzen, müssen diese Variablen zunächst auf eine gemeinsame Skala umgerechnet werden. Hier von 0 bis 1.
Das ist ein hemdsärmeliges Verfahren! Statistikprogramme wie SPSS erledigen das – bei richtiger Vorgabe – automatisch. Aber nicht jeder hat es (ich übrigens auch nicht; ich benutze sonst etwas anderes). Das von mir gewählte Verfahren kann jeder selbst nachrechnen. Zumindest theoretisch. Es erfordert einigen Aufwand (und das ist wirklich nicht harmlos gemeint), aber es ist möglich.
Um die normalisierten Werte miteinander in Beziehung setzen zu können, müssen die Werte noch ein weiteres Mal umgeformt werden.
Ich will das näher erklären:
Zugrunde liegen zum Beispiel zunächst folgende zu überprüfende Hypothesen;
- Mehr Covid-Tote bei höherem Anteil Menschen ab 80 Jahren
- Mehr Covid-Tote bei niedrigeren Durchschnittstemperaturen
- Mehr Covid-Tote bei weniger verabreichten Impfdosen
Korrelationen mit mehreren Variablen können nicht ohne Weiteres berechnet werden, wenn bei einer Variablen ein positiver Zusammenhang vermutet wird und bei einer anderen ein negativer. Das würde sich gegenseitig aufheben.
Sie müssen so umgeformt werden, dass alle Hypothesen entweder positiv sind oder negativ. Gemischt werden können sie aber nicht.
Um diese Variablen gemeinsam miteinander in Beziehung setzen zu können, müssen sie also so umgerechnet werden, dass folgende Hypothesen (vor allem in der Addition) mit gleichem Vorzeichen überprüft werden können:
- Mehr Covid-Tote bei höherem Anteil Menschen ab 80 Jahren
- Mehr Covid-Tote bei höherer Abweichung von der maximalen Durchschnittstemperatur
- Mehr Covid-Tote bei höherer Abweichung von der maximalen Anzahl der verabreichten Impfdosen.
Es sind im Grunde die gleichen Hypothesen, nur sind sie anders formuliert, um rechnerisch die gleichen Vorzeichen zu erhalten.
Das Abrufdatum der Daten ist wie folgt:
Bundesamt für Statistik (Bevölkerung & Todesfälle allgemein): 23.01.2022
Robert-Koch_Institut (Covid-Todesfälle): 27.01.2022
Deutscher Wetterdienst (Temperaturdaten): 05.02.2022
Dargestellt sind Daten bis inklusive der Kalenderwoche 3/2022.
Zusammenhang zwischen dem Anteil der Menschen ab 80 Jahren und der Höhe der Covid-Toten
Nun zur eigentlichen Intention dieses Beitrages. Wie schon damals im Juli 2020 auf internationaler Betrachtungsebene, soll nun auf der Ebene der deutschen Bundesländer ein möglicher Zusammenhang zwischen dem Anteil der Bevölkerung ab 80 Jahren und der Zahl der Covid-Toten untersucht werden.
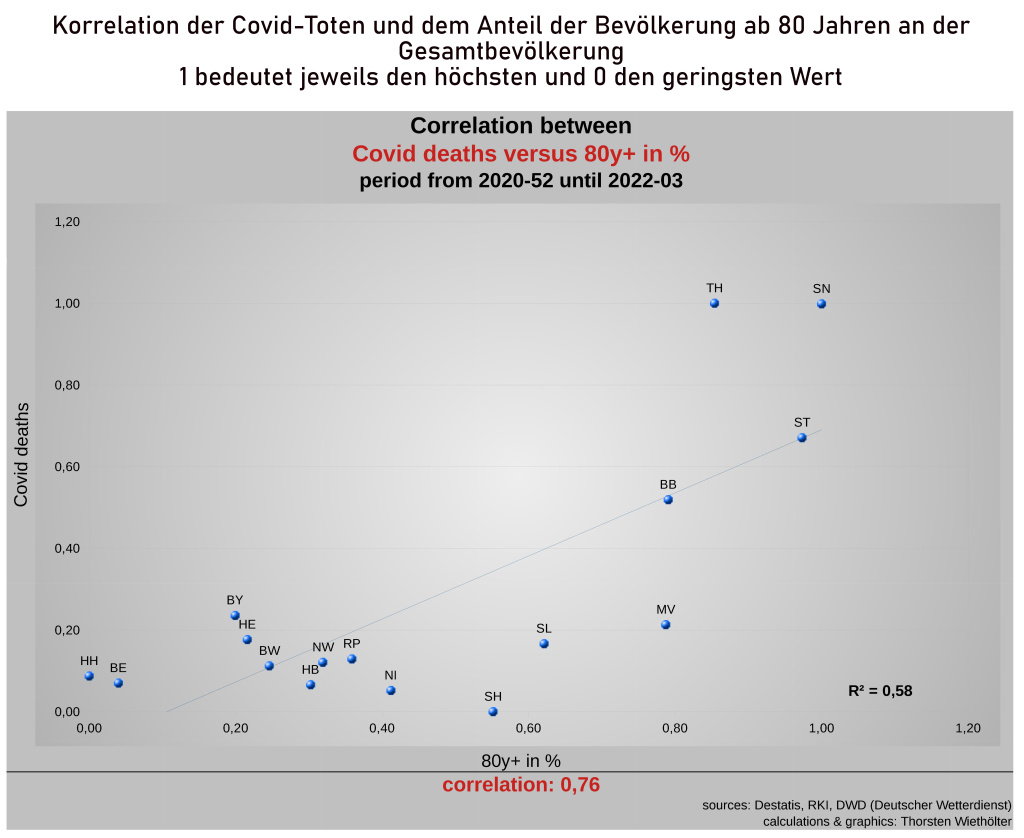
In der folgenden Grafik ist die Korrelation der Covid-Toten pro 100 Tausend der jeweiligen Bevölkerung gegenüber dem jeweiligen Bevölkerungsanteil der ab 80-Jährigen dargestellt. Der Zeitraum ist von Woche 52/2020 (Beginn der Impfungen) bis zur Woche 03/2022 (bisher verfügbare Daten).

Die Korrelation von 0,76 ist recht stark und damit ist ein Zusammenhang zwischen Covid-Toten und dem Anteil der Bevölkerung über 80 Jahren kaum von der Hand zu weisen. Aufgrund logischer Überlegungen vermuten kann man es sowieso.
Zusammenhang zwischen Klima und der Höhe der Covid-Toten
Als Indikator für den sehr weit gefassten Begriff ″Klima“ wurden hier die Durchschnittstemperaturen der Bundesänder herangezogen und untersucht, ob ein Zusammenhang mit der Anzahl der Covid-Toten anzunehmen ist oder nicht.
Als Referenzdurchschnittstemperatur in der folgenden Grafik wurde diejenige des Januars 2021 herangezogen. Das kann auf den ersten Blick als unzureichend bewertet werden, aber ich konnte feststellen, dass genau dieser Wert ein guter Referenzwert ist, weil er hohe Korrelationen zu allen anderern Temperaturwerten darstellt, sei es zur Durchschnittstemperatur des Gesamtjahres als auch zu anderen vergleichbaren Werten.

Auch in der Beziehung von Durchschnittstemperaturen pro Bundesland und der Anzahl der Covid-Toten kann also ein Zusammenhang als wahrscheinlich angenommen werden. Die Korrelation von 0,62 ist vergleichsweise hoch, das Bestimmtheitsmaß von 0,39 eher so làlá. Das ist aufgrund der unterschiedlichen Größe und Klimazonen der Bundesländer, die sich nicht an offizielle Bundeslandgrenzen halten aber gar nicht mal so unerwartet.
Besonders interessant wird es im folgenden Abschnitt, in dem die Zahl der Covid-Toten in Beziehung zum Bevölkerungsanteil ab 80 Jahren UND den Temperaturen gesetzt wird.
Zusammenhang zwischen den Covid-Toten und der Kombination aus der Bevölkerung ab 80 Jahren und der Durchschnittstemperatur
Wenn man nun den Anteil der Bevölkerung ab 80 Jahren und die durchschnittlichen Temperaturen (im Januar 2021) miteinander kombiniert, kommt (im Zeitraum seit Beginn der Impfungen) folgende Korrelationsbeziehung heraus:

Wenn Durchschnittstemperatur und der Anteil der Bevölkerung über 80 Jahre addiert werden, dann ergibt sich eine Korrelation von 0,88 mit der Anzahl der Covid-Toten. Die Covid-Toten können also zu 88% durch die beiden Faktoren Durchschnittstemperatur und Anteil der ab 80-Jährigen vorhergesagt werden. Das ist ganz offensichtlich ein hoher Wert!
Obwohl – wie oben erwähnt – die Signifikanzberechnung fehlt, denke ich, diese Bewertung vornehmen zu können. Zu dieser Einschätzung kann man übrigens ebenfalls rein durch logische Betrachtung kommen. Dass es aber dennoch von Bedeutung ist, dies statistisch darzustellen, wird hoffentlich im weiteren Verlauf klar.
Zusammenhang zwischen Covid-Toten und Impfungen
In letzter Zeit muss ich immer häufiger davon lesen, dass ein Zusammenhang zwischen der Höhe der Impfquote und einer geringeren Anzahl an Covid-Toten ″bewiesen“ sei. Das Magazin ″Focus“ schreibt gar von ″knallharten Fakten“. Und komischerweise öffnet hier – soweit es mir bekannt ist – niemand die bereits oben erwähnte verrostete Kellertür zum Arsenal der statistischen Waffen.
Es ist vollkommen richtig, dass es einen Zusammenhang in dem Sinne zu geben scheint, dass Bundesländer mit höheren Impfquoten niedrigere Covid-Todeszahlen aufweisen. Das habe ich selbst ebenfalls errechnet.
Die diesbezügliche Grafik für den Gesamtzeitraum seit Beginn der Impfungen sieht so aus:

Mit einer Korrelation von 0,79 scheint die positive Wirkung der Impfung kaum von der Hand zu weisen zu sein.
″Knallharte Fakten“ sind das allerdings nicht! Denn auch, wenn dies für das Narrativ ″Impfung wirkt“ spricht, halte ich es für notwendig, dies zu überprüfen.
Es ist nicht so, dass ich eine positive Wirkung der Impfung von vorneherein bestreiten will. Ich halte sie grundsätzlich für möglich! Allerdings weiß ich nicht, in welchem Maße und für wie lange und habe hier begründete Zweifel. (Anmerkung: Ich spreche hier nur von möglichen positiven Wirkungen der Impfung, nicht von negativen.) Außerdem können internationale Vergleiche durchaus auf den ersten Blick ganz andere Annahmen vermuten lassen.
Ohne darauf hier näher einzugehen, sei als Beispiel und nur zur Veranschaulichung der Musterknabe Israel dargestellt:

Desweiteren ist es nun einmal so, dass auch ganz andere Faktoren statistisch hinreichend die Anzahl der Covid-Toten erklären können – vollkommen ohne Einbezug der Impfungen – , wie man oben sehen kann.
Der Anteil der Menschen ab 80 Jahren und die Durchschnittstemperaturen sind unabhängig von anderen Einflussfaktoren. Sie sind sozusagen ″unschuldige“ Faktoren, weil sie nicht so leicht manipulierbar sind und im Sinne des Covid-Narrativs kaum im Fokus stehen. Die Anzahl der Covid-Toten muss man als gegeben nehmen, weil sie einfach so erhoben wurden. Ob die Zahlen nun richtig sind oder nicht. Allerdings wäre natürlich zu hinterfragen, inwiefern Geimpfte oder gar Geboosterte überhaupt noch getestet werden. Allein hierin kann nämlich schon die Gefahr einer Scheinkorrelation liegen, wenn nämlich Geimpfte mit geringerer Wahrscheinlichkeit getestet werden als Ungeimpfte, was dann auch diejenigen betreffen kann, die in der Folge versterben. Dadurch würde nämlich automatisch ein statistischer Zusammenhang zwischen hoher Impfquote und niedriger Covid-Todesrate kreiert, der aber auf der Testmethodik beruht und nicht auf der Krankheit selbst. Gehen wir der Einfachheit halber einfach mal davon aus, dass die Zahlen korrekt seien und es keinen Testmethodik-Unterschied zwischen Geimpften und Ungeimpften gäbe.
Die Faktoren Alterstruktur und Durchschnittstemperatur existierten schon in 2020, sind also keine neuen Variablen. Sie können zwar leicht andere Werte gehabt haben, sollten aber keinen signifikanten Veränderungen unterliegen.
Bezüglich der Impfungen kommt aber eine Besonderheit hinzu: Diese sind der einzige Faktor, der vollkommen neu ist. Die Covid-Impfungen gab es 2020 (bis zur KW 51 und außer in Studienpopulationen) noch gar nicht und sie spielten erst 2021 eine Rolle, und zwar erst sukzessive mit der Zunahme der verabreichten Impfdosen.
Aufgrund der Bedeutung, die den Impfungen zugeschrieben wird, sollte doch angenommen werden können, dass diese neue Variable zusätzlich zum Anteil alter Menschen und den Durchschnittstemperaturen die Korrelation zu der Zahl der (verringerten) Covid-Toten stärker macht, nicht wahr?
Das tut sie aber nicht.

Obwohl isoliert gesehen eine positive Korrelation zwischen der Anzahl der Impfungen und einer verringerten Anzahl an Covid-Toten besteht, führt die Variable der Impfungen zu keiner relevanten Verstärkung der Korrelation zwischen den Covid-Toten und der Kombination von Altersanteil und Temperaturdurchschnitt. (Korrelation Alter und Temperatur: 0,88 versus 0,89 Korrelation Alter, Temperatur und Impfquote)
Ausgeschlossen ist eine positive Wirkung der Impfung auf die Höhe der Covid-Toten natürlich trotzdem nicht, Aber es kann ebenfalls nicht ausgeschlossen werden, dass es sich bei der Korrelation zwischen Anzahl der Impfungen und Covid-Toten um eine Scheinkorrelation handelt.
Dass dieser Gedankengang durchaus seine Legitimation hat, kann ich belegen! Und zwar mit dem einfachen Beispiel, dass man den Zeitraum seit Beginn der Impfungen in der Woche 52/2020 bis zur Woche 03/2022 (letzte verfügbare Daten) auswertet und dann zum Vergleich …die Covid-Toten im Jahr zuvor gegenüberstellt.
Und das wird hier nun dargestellt. Es wird also die Impfquote bis zur Kalenderwoche 03/22 pro Bundesland den Covid-Toten bis zur Woche 03/21 gegenübergestellt. Also die aktuelle Impfquote gegenüber den Covid-Toten im Zeitraum eines Jahres zuvor.

Ups, was ist denn das für eine mächtige Korrelation?!
Der entscheidende Punkt ist aber: Wie kann denn die Impfquote eines Jahres die Covid-Toten eines anderen, vergangenen Jahres rückwirkend beeinflussen, in dem noch gar nicht (bzw. fast gar nicht) geimpft wurde?
Richtig, Sie ahnen es! Es handelt sich um eine Scheinkorrelation. Und bei dieser Betrachtung sogar um eine bewiesene Scheinkorrelation, denn es ist vollkommen unmöglich, dass die Covid-Toten rückwirkend im Jahr 2020 mit der Impfquote Ende 2021/Anfang 2022 zusammenhängen.
Für das Jahr 2021 bedeutet dies dann auch im Folgeschluss: Die Wirkung der Impfung lässt sich so also weder belegen noch widerlegen.
Es bleibt dennoch die Erkenntnis, dass sich die Zahl der Covid-Toten auch hinreichend durch andere Faktoren – ohne Einbezug der Impfungen – erklären lässt.
Es gibt eine weitere Seltsamkeit, die indirekt eine Scheinkorrelation bei den Impfungen begünstigen könnte:
Unabhängig von den Impfungen ist es denkbar, dass schwerere Erkrankungswellen (und damit auch Tote) in der Vergangenheit zu milderen Wellen in der Gegenwart führen können, weil in der Vergangenheit eine höhere Herdenimmunität aufgebaut wurde und vulnerable Menschen tragischerweise bereits vor ihrer Zeit verstorben sind. Man könnte also schlussfolgern, dass Bundesländer, die in der Vergangenheit höhere Covid-Todeszahlen hatten, nun geringere Zahlen haben. Um dies zu überprüfen, können die Todeszahlen der 4. Welle mit denen der vorherigen Wellen verglichen werden.
Zur Einordnung hier der Verlauf der Covid-Todeszahlen in Deutschland insgesamt:

Die Abgrenzung der Wellen wurde nach dem jeweilig geringsten Auftreten von Covid-Toten vorgenommen.
Wenn man nun die vierte Welle mit der Summe der vorangegangenen Wellen vergleicht, dann kommt aber ein vollkommen unerwartetes Ergebnis heraus – jedenfalls für mich. Diese hohe Korrelation zwischen den Covid-Toten der vierten Welle mit denen der vorangegangenen Wellen bedeutet nämlich, dass Bundesländer, die in der Vergangenheit viele Covid-Tote hatten, auch in der aktuellen Welle wieder hohe Todeszahlen haben und eben nicht niedrigere.

Um ehrlich zu sein: Eine derartige Korrelation ist schon bemerkenswert!
Und: Das weist nicht unbedingt auf einen besonders wirkungsvollen Effekt der Impfung hin (ohne ihn allerdings auch zu widerlegen!). Es bekräftigt aber, dass eine reine Korrelationsberechnung von Impfquote und Covid-Todeszahl im Jahr 2021 sinnlos ist. Allerdings kann es eine Indikation dahingehend sein, dass Alter und Temperatur wichtige und stabile Einflussfaktoren sind. Immerhin muss irgendein Faktor vorliegen, der die Höhe der Covid-Toten beeinflusst und der sowohl in 2020 als auch in 2021 ähnlich stabil und stark gewesen ist. Und das sind selbstverständlich nicht die Impfungen. Als weitere mögliche Einflussfaktoren kämen unter anderen z. B. unterschiedliche Erhebungs- und Teststrategien in den Bundesländern in Frage, die aber in 2020 und 2021 im jeweiligen Bundesland ähnlich gewesen sein müssten oder ähnlich unterschiedlich zu denen anderer Bundesländer gewesen wären. Auf jeden Fall lassen solche Korrelationsmuster keinen Rückschluss auf die Effektivität der Impfungen zu.
Apropos Scheinkorrelationen
Vor ein paar Wochen postete ich auf Twitter eine Grafik, die die Impfdosen und die Sterblichkeitsveränderungen gegenüberstellte. Etwa zur gleichen Zeit, als Prof. Dr. Kuhbandner eine Studie zu eben diesem Thema veröffentlichte (Quelle: https://osf.io/5gu8a/).
Ich kam zu ähnlichen Ergebnissen wie er selbst. Aber seitdem wurde er überzogen von übermäßiger Kritik.
Ich kenne nicht die genaue Methodik von Prof. Dr. Kuhbandner. Insofern kann ich mich nicht detailliert dazu äußern, aber die Kritik an seiner Analyse kann ich in der vorgenommenen Art und Weise so nicht nachvollziehen. Mittlerweile wurde seine Analyse sogar als ″Unstatistik des Monats“ vom RWI – Leibniz-Institut für Wirtschaftsforschung – aufgenommen (https://www.rwi-essen.de/unstatistik/123/).
Die Ausführungen im Artikel vom RWI sind technisch zwar aus meiner Sicht vollkommen korrekt und ich bin davon überzeugt, dass die dortigen Experten wissen, worüber sie schreiben. Dennoch bin ich damit nicht einverstanden, denn der Artikel insinuiert, dass Kuhbandners Darstellungen Scheinkorrelationen sind. Das ist aber genauso falsch, als würde man Kuhbandners Darstellungen als unwiderlegbaren Beweis eines Zusammenhangs zwischen Impfungen und Übersterblichkeit nehmen. (Was er selbst meines Wissens übrigens nicht getan hat.)
Die Gefahr von Scheinkorrelationen besteht, aber es heißt nur, dass es Scheinkorrelationen sein können.
Gleichzeitig bezieht sich das RWI wiederum auf Studien, die auf Daten beruhen, die ganz und gar nicht ohne Weiteres als statistisch vertrauenswürdig betrachtet werden können. Und die im Artikel genannten Beispiele für Scheinkorrelationen sind zwar korrekt, aber abstrus.
Es ist allerdings richtig, dass bei sogenannten nicht-stationären Datenreihen, also z. B. Zeitreihen mit einem (saisonalen) Trend, eine hohe Gefahr von Scheinkorrelationen bestehen kann. Ein Grund dafür ist z. B., dass dieser Trend beide in Beziehung gesetzte Variablen gleichermaßen beeinflusst und dann nicht die Korrelation der Variablen zueinander gemesssen wird, sondern die Korrelation, die die Variablen mit dem gemeinsamen Trend oder einer gemeinsamen (möglicherweise unbekannten) Variablen haben. Und es ist richtig, dass Sterbezahlen einem saisonalen Trend unterliegen.
Was meine eigene Betrachtung angeht, so kann ich aber sagen, dass mir diese Problematik durchaus bewusst ist. Daher habe ich, bezogen auf die Sterbefälle, den saisonalen Trend wie folgt möglichst neutralisiert:
Zunächst wurden die wöchentlichen Sterberaten seit der Kalenderwoche 01/2016 bis zur Kalenderwoche 52/2021 anhand der vorhandenen Bevölkerungszahlen pro Altersgruppe errechnet.
Im nächsten Schritt wurden die Sterbefälle aller Jahre auf die Bevölkerungstruktur des Jahres 2021 normiert. Konkret heißt das, es wurde errechnet, wieviele Menschen in den vergangenen Jahren verstorben wären, wenn die Bevölkerungszahl und Alterstruktur die gleiche wie die des Jahres 2021 gewesen wäre.
Danach wurde errechnet, inwieweit die wöchentlichen Sterbefälle im Jahr 2021 von einem Erwartungswert abweichen. Dieser Erwartungswert sind die theoretischen Sterbefälle in den Jahren 2016 bis 2019 bei gleicher Bevölkerungszahl und Altersstruktur wie in 2021. Damit wird ein saisonaler Trend weitgehend neutralisiert, da zum Beispiel der Erwartungswert in einer beliebigen Woche im Winter sich aus Vergangenheitswerten ergibt, die ebenfalls in der gleichen Woche im Winter liegen usw. Um es anschaulicher zu machen: Wenn – theoretisch – die Sterblichkeit in 2021 die gleiche gewesen wäre wie im Durchschnitt der Jahre 2016 bis 2019, dann würden die Abweichungen des Jahres 2021 immer stabil um eine Nulllinie liegen. Tun sie es nicht, dann stimmt etwas nicht, oder ein neuer Faktor spielt eine Rolle.
Aufgrund der Tatsache, dass die Corona-Pandemie ein neues Phänomen ist, das bis 2019 noch nicht vorhanden war und der sich aus diesem Umstand ergebenden Vergleichsverzerrung, wurden die Covid-Toten herausgerechnet und die Non-Covid-Sterbefälle betrachtet. Aus dem gleichen Grund wurde das Jahr 2020 nicht in die Durchschnittsrechnung aufgenommen, sondern separat gerechnet.
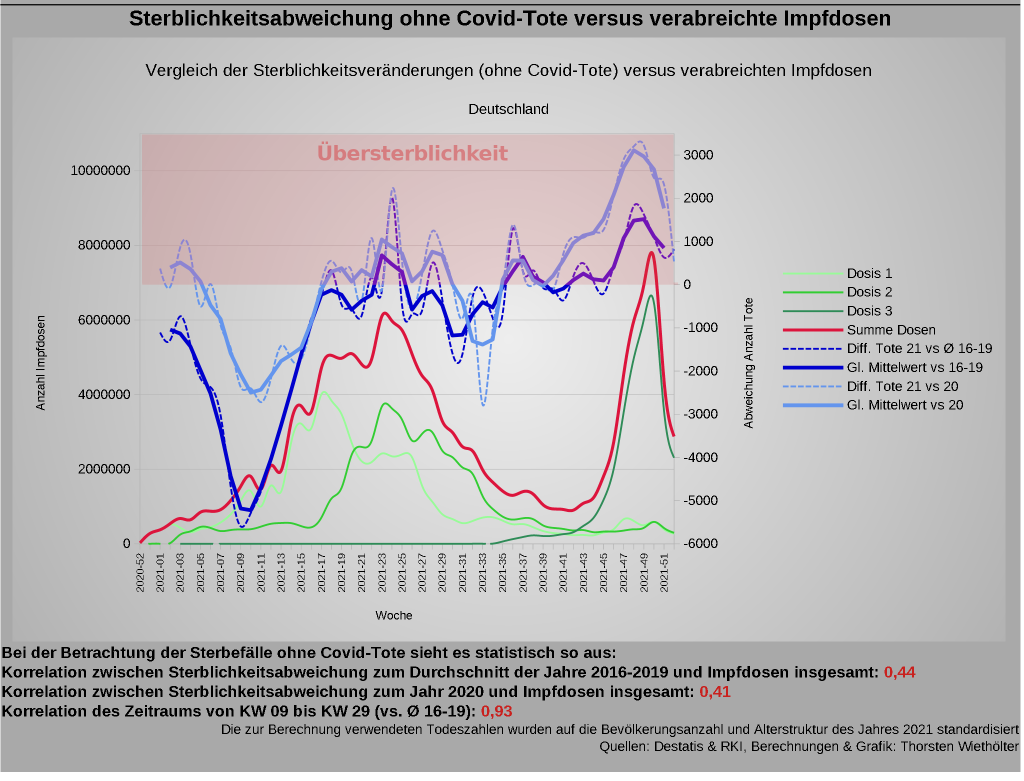
So stellen sich die Daten dar:

Anmerkung zu der auffälligen Untersterblichkeit mit dem Höhepunkt in der Kalenderwoche 09/2021: Natürlich kann man davon ausgehen, dass, wenn während einer Infektionswelle mehr Menschen verstorben sind, als es üblich ist und es statistisch vor ihrer Zeit ist, dass dann in der Folge zunächst eine Untersterblichkeit eintreten kann und diese sogar wahrscheinlich ist. Und im Winter 2020/21 war offiziell eine starke Infektionswelle. Die Herausrechnung von Covid-Toten ändert natürlich nichts an den Untersterblichkeiten, weil man Menschen, die zu einem bestimmten Zeitpunkt nicht verstorben sind, auch von nichts abziehen kann.
Auffällig ist jedenfalls, dass seit der Woche 16/2021 häufiger eine Übersterblichkeit vorliegt (besonders gegenüber dem Jahr 2020), die sich um die Woche 35 verstetigt. Wenn es nachvollziehbare Gründe dafür gibt, dann würde ich sie wirklich gerne kennen.
Je nachdem, welche Zeiträume nun betrachtet werden, ergeben sich zum Teil sehr hohe Korrelationen. Ist dies eine Scheinkorrelation? Möglich. Ich kann nicht beweisen, dass es nicht so ist. Aber es stellt sich dann die Frage, welcher Trend, welche Saisonalität oder welche unbekannte gemeinsame Variable zu dieser Korrelation führt. Mir fällt dazu wirklich nichts Plausibles ein.
Reiner Zufall? Ich kann weder belegen noch widerlegen, dass es so ist.
Aber mal Hand aufs Herz: Ein solcher – teilweise viel zu paralleler – Kurvenverlauf ist ein Alarmsignal, das man nicht einfach so abtun kann. Anstatt nur über rein theoretische statistische Methodiken zu diskutieren (was natürlich trotzdem richtig und wichtig ist), gehört es sich einfach, einem solchen Muster mit allen zur Verfügung stehenden Mitteln nachzugehen! Das gebietet allein schon der gesunde Menschenverstand, der Wunsch nach Erkenntnis und ein Minimalinteresse daran, Menschen keinen Schaden zuzufügen.
Quellen:
Bevölkerungsfortschreibung Bundesländer
Bevölkerung: Bundesländer, Stichtag, Altersjahre
Bevölkerungsvorausberechnung Bundesländer
Vorausberechneter Bevölkerungsstand: Bundesländer, Stichtag,
Varianten der Bevölkerungsvorausberechnung, Geschlecht, Altersjahre
Bevölkerungsvorausberechnung Bundesländer, Ausblick nach Corona
Ausblick auf die Bevölkerungsentwicklung in Deutschland und den Bundesländern nach dem Corona-Jahr 2020 – Erste mittelfristige Bevölkerungsvorausberechnung 2021 bis 2035
Sterbefallzahlen
Deutscher Wetterdienst (DWD), Zeitreihen der Durchschnittstemperaturen pro Bundesland
https://www.dwd.de/DE/leistungen/zeitreihen/zeitreihen.html?nn=18256#buehneTop
RKI Impfdatentracking
https://github.com/robert-koch-institut/COVID-19-Impfungen_in_Deutschland
Danke für Ihre ausführlichen Betrachtungen!
LikeGefällt 1 Person
Vielen Dank für Ihr Interesse!
LikeLike
Die Zeit der Unterbrechung der Übersterblichkeit in 2021 (KW 30-max. 34) entspricht der Kernzeit der Sommerferien. Ob das vielleicht einen Einfluss hat auf bestimmte Bevölkerungsgruppen, die zu dieser Zeit nicht geimpft worden und dadurch auch keinem UAW Risiko ausgesetzt waren, ist für mich unklar.
LikeLike
Das ist möglich. Aber zur besseren Analyse müsste man die Daten insgesamt altersgruppenspezisch betrachten können. Nur leider habe ich keinen Zugang zu Impfzeitreihen, die nach Altersgruppen aufgeschlüsselt sind.
LikeLike
Auch von meiner Seite einen herzlichen Dank für den überaus sachlichen und informativen Beitrag, hinter dem sehr viel Arbeit steckt. Ganz unabhängig davon, wie man zu den Impfungen steht (ich persönlich meine, dass es so viele Anhaltspunkte für eine mögliche erhebliche Gefährlichkeit der Impfstoffe gibt, dass eine breite Diskussion zwingend nötig wäre), krankt der öffentliche Diskurs vor allem an ernsthaften und echten Diskussionen. Ihre Untersuchung leistet hierfür jedenfalls einen ganz wichtigen Beitrag.
LikeGefällt 2 Personen
Vielen Dank für Ihren Kommentar! Ja, ich bin ebenfalls der Meinung, dass eine breite Diskussion zwingend, und auch dringend, nötig wäre.
LikeLike
Können Sie kurz erläuteren, warum bei dem letzten Diagram „Steblichkeitsabweichung ohne C-Tode vs. verabreichte Impfdosen“ die Nulllinie der rechten Ordinate „Abweichung Anzahl Tode“ nicht mit der rot-schraffierten „Übersterblichkeit“ zusammenfällt? Die rot-schraffierte Box „Übersterblichkeit“ beginnt ja bereits bei ca. – 800; müsste doch eigentlich bei 0 beginnen (>0 positive Abweichung Anzahl Tode),oder ist die Ordinaten-Beschriftung der rechten Seite verrutscht? Wenn die Übersterblichkeit (rot-schraffierte Box) bei >0 begänne, sehe es gar nicht mehr „so“ dramatisch aus…
LikeLike
Ganz vielen Dank für Ihren Kommentar! Da ist mir nämlich ein Fehler unterlaufen. Die rote Fläche habe ich nachträglich mit einem Grafikprogramm hinzugefügt und sie bezieht sich auf zwei Diagramme, eins zur Gesamtsterblichkeit und eins zur Non-Covid-Sterblichkeit. Das zweite Diagramm (Non-Covid-Sterblichkeit) hat aber nicht die gleiche Skalierung. Ich werde das korrigieren.
LikeLike
Sehr geehrter Herr Wiethölter,
vielen Dank für die Mühe des Artikels, bzw. der Rechnungen und der grafischen Aufbereitung.
Mein Wunsch an Sie: melden Sie sich doch einmal bei Professor Kuhbandner und fragen Sie ihn nach seinem Rechenweg. Ich glaube, dass er Ihnen sehr gern Auskunft gäbe und es im besten Falle zu einem fruchtbaren Austausch käme, der dann auch für uns als Konsumenten, wieder einen Mehrwert bringt.
Bitte bleiben Sie dran und lassen Sie sich nicht runterschreiben 🙂
LikeGefällt 2 Personen
Vielen Dank für die Anregung!
Ja, daran habe ich durchaus schon gedacht. Aber ich habe im Moment gar keine konkreten Fragen. Im Prinzip sind mir seine Erläuterungen schon klar und soweit auch verständlich. Darüber hinaus ist alles auch eine Zeitfrage (sowohl für ihn als auch für mich.) Und ich finde, dass seine Analysen einfach Grund genug sind, all dem genauer nachzugehen. Dass solche Analysen immer auch irgendwie angreifbar sein können, ist mir ebenso klar. Dass sie deshalb einfach nur abgetan werden aber nicht! Das halte ich für billig und sogar richtiggehend zynisch. Das eigentliche Problem liegt meiner Meinung nach aber vor allem in einer erschreckend schlechten und unfassbar rudimentären Qualität offizieller Daten, die ich früher nie für möglich gehalten hätte, und aufgrund derer dann sogar noch krasse politische Entscheidungen getroffen werden, die massiv das Leben und die Grundrechte von Menschen betreffen, die sich kaum dagegen wehren können. Für mich ist das alles so eine Art Mittelalter 2.0. (Nur technisch moderner, was es sogar noch viel schlimmer macht.) Meine Fassungslosigkeit darüber kann ich gar nicht mehr in Worte fassen.
LikeGefällt 1 Person
Seit dem 21.02.2022 gibt es eine ausführliche Stellungnahme von Prof. Dr. Kuhbandner zu den Vorwürfen:
„Der Anstieg der Todesfälle im zeitlichen Zusammenhang mit den Impfungen: Ein Sicherheitssignal wird ignoriert
Ende Januar veröffentlichte der Regensburger Psychologieprofessor Christof Kuhbandner eine 28-seitige Untersuchung, die einen alarmierenden zeitlichen Zusammenhang zwischen der Zahl der verabreichten COVID-Impfungen und der Anzahl der offiziell registrierten Todesfälle in Deutschland belegt. Ein österreichischer Fernsehsender berichtete darüber. In der vergangenen Woche veröffentlichten nun der Bayerische Rundfunk und die Nachrichtenagentur dpa Faktenchecks, wonach die Berechnungen fehlerhaft seien. Prof. Kuhbandner reagiert hier erstmals ausführlich auf die Vorwürfe und kritisiert seinerseits fragwürdige statistische Argumente der Kritiker sowie eine unsachgemäße und irreführende Aufbereitung des Sachverhalts in den Medien.“
https://multipolar-magazin.de/artikel/ein-sicherheitssignal-wird-ignoriert
LikeLike
Ja, den Artikel habe ich gestern gelesen und ich stimme ihm zu.
LikeLike
Die statistische Betrachtung in Ehren, aber es ist auf Grundlage der erhobenen Daten nicht aufzeigbar was tatsächlich vor sich geht. Ich möchte ihnen Einflussfaktoren nahe legen, die ihrer Betrachtung fehlen und noch ein paar Dinge darüber hinaus schreiben.
Erstes Beispiel, hat die „Angst vor Corona“ dazu geführt, dass es zu weniger Interaktion der Menschen miteinander kam und allgemein weniger Aktivität da war. Nehmen wir einrichtungsbezogenen Sport, allgemein Sport oder auch Vereinssport. Zum einen werden weniger Tote zu beklagen sein, die beim Sport sich bis hin zum Tode verletzt haben, weil sie nunmal daheim geblieben sind. Zum anderen ist das ausbleiben von Sport zeitlich verzögert eine gesundheitliche Verschlechterung, die wiederum zu mehr Toten in der Folgezeit führt. Der Einflussfaktor ist statistisch nicht herausrechnbar, abbildbar, weil es dafür keine Datengrundlage mit einer Vergleichsgruppe gibt, mit der man den Faktor herrausrechnen könnte.
Zweites Beispiel, im Rahmen der Corona-Bereitschaft haben Krankenhäuser Operationen abgesagt, verschoben etc. Allein dadurch sind zig tausende die an Fehlbehandlungen gestorben wären länger am Leben gewesen, als sie statistisch es hätten sein dürfen. Zugleich gibt es aber wegen der verschobenen Operationen auch Nachholeffekte nach nunmehr 2 Jahren, dass etwa ein Tumor der nicht entfernt wurde oder eine Transplantation die nicht stattfand, nun den Patienten umgebracht hat, der aber ggf. noch länger gelebt hätte, wäre der Eingriff erfolgt.
Zudem ist jeder Mensch der nicht in ein Krankenhaus geht auch nicht konfrontiert mit der Problematik von „resistenten Keimen“. Ergo sterben daraus folglich weniger Menschen. Nun kommen aber gleichsam mit Atemwegsinfekten vermehrt Leute in die Klinken zur Behandlung, deren Immunsystem schon mit dem Erreger der den Infekt ausgelöst hat beschäftigt sind. Mit der Anwesenheit von den entsprechenden multiresistenten Keimen und dem Fokus auf „Covid“ kann es eine Menge Leute in der Umgebung dahingeraft haben. Die Attribution Covid ist dem Augenmerk darauf gerichtet. Ursächlich am Tod mag aber der Krankenhauskeim gewesen sein, den der Patient sich erst dort eingefangen hat. Zudem gehen wir mal nicht auf die Problematik ein das die Behandlungsprotokolle für Covid bis heute uneinheitlich sind, je nach dem ob der behandelnde Arzt Ivermectin, Hydroxclroquin, monoklonale Antikörper für die Behandlung verwendet oder nicht und ob er es mit einem Coronaleugner zu tun hat oder mit einem Impf-„Trust the science“-Patienten und wie er selbst zur Thematik steht.
Dritter Einflussfaktor, den sie angekratzt haben, aber nicht relevant in die Betrachtung einbezogen haben, nämlich die Datengrundlage wer wann als Covid erkranker gilt. Die Unterscheidung in der Anzahl der Testzyklen der PCR-Testung. die zwischen geimpften und ungeimpften getroffen wird, hat hier eine maßgeblichen Anteil auf die Verzerrung der Daten. Würde es keine Unterscheidung geben und zudem alle PCR Testlabore geeicht sein (sind sie nicht!!!!!!!) könnte man von Daten sprechen, die sinnvoll in Bezug zu setzen wären zu anderen. Aber Coronatote, sind über den Betrachtungszeitraum, nicht nach den selben Regeln als solche verifiziert wurden. Es ist Datensalat, allein dahingehend betrachtet, das Impfbefürwortende Ärzte, in ihrer subjektiven Realität geimpfte Tote nicht als Corona-Tote ausgewisen haben werden! Den es darf nicht sein, was nicht seien kann, im Bullshitbingo um comorbide Patienten die verstorben sind.
Mit Müll Statistik zu machen ist zwar schönes Zahlenschubsen, hat aber keinen Bezug zur Realität!
Seit zwei Jahren wurden Milliarden aufgewendet im Rahmen der Corona Pandemie, aber es waren keine Millionen vorhanden aussagekräftige Studien zur Begleitung zu erstellen (Wer in welcher Altersgruppe nach geschlecht getrent, Wann mit welcher Viruslast, Wie medizinisch schwerwiegend, Wo mit Was für Nebenkrankheiten, Warum die Krankheit nicht oder doch überstanden hat), noch eine Erfassung dessen was vor sich geht in einer als so problematisch erklärten Pandemie relevant medizinisch zu erfassen während man experimentelle Impfungen verabreicht (Wie hat sich welche Impfdosierung zu welchem Zeitpunkt in welcher Altesgruppe im Vergleich zu einer ungeimpften Vergleichsgruppe mit welchen Nebenerkrankungen und welchen Behandlungsmethoden in Was für Nebenwirkungen, Heilungen oder Nichterkrankungen zeitlich abgebildet) Inklussive erfassung von Immunologischen Grunddaten (IgG, IgM, Titer seit bekanntwerden von Blutgerinnungen und weiterer Werte hinsichtlich der Karzogenität).
Deutschland ist wie immer Spitzenreiter im „im Dunklen tappen“ und darüber hinaus an seiner nicht vorhandenen Digitalisierung gestolpert und leider sind wir damit nicht allein. VAERs verzeichnet für Östterreich zuletzt mehr Tote als Impfkomplikation als die Statistik der Österreichischen Behörden ausweist, die genau den selben Sachverhalt ausweisen soll. In Deutschland wird das kein deut besser sein! Wer auf solchen nichtvorhandenen Datengrundlagen Aussagen macht, stochert im Nebel, der absichtlich nicht beseitigt werden soll, den es gibt genug Forderungen ordentlich Daten zu erfassen seit BEGINN dieser vermeinten Pandemie.
LikeLike
Was auch immer Sie von meinem Beitrag halten mögen: Wenn ich statistische Zusammenhänge darstellen will, dann muss ich nun einmal die Daten verwenden, die zur Verfügung stehen. Ich kann mir keine Daten aus den Fingern saugen.
Im Übrigen steht mein Beitrag nicht automatisch im Widerspruch zu Ihren Hypothesen. Einige davon würde ich mir sogar zu eigen machen. Wenn ich etwas nicht behandle, dann wäre die Schlussfolgerung daraus, dass ich es deshalb negiere, einfach falsch. Nur! Ich kann sie nicht unbedingt belegen. In meinem Beitrag ging es mir aber tatsächlich um statistisch spezifisch darlegbare Zusammenhänge, deren Limitationen oder deren mögliche Fehlschlüsse, und nicht um die Aufzählung aller Hypothesen, die in Frage kommen könnten. (Da gäbe es übrigens noch weitaus mehr.) Ich würde mich aber sehr freuen, wenn es Ihnen gelänge, die von Ihnen genannten Hypothesen zu untermauern. Diese Bürde kann ich Ihnen leider nicht abnehmen. Ich fürchte, dass hier einfach ein Missverständnis über die eigentliche Intention meines Beitrags besteht.
LikeLike
Das kann durchaus ein Missverständnis sein. Nochmal vorangestellt halte ich es für einen sehr wichtige Beitrag diese Korrelationen der Öffentlichkeit aufzuzeigen. Einige werden es weniger verstehen andere umso besser. Jedenfalls ist es ein Anknüpfungspunkt für Weiteres.
Ich denke oder würde davon ausgehen, dass wenn ich eine Betrachtung zu Einflussfaktoren mache und habe etwa 80% gut erklärlich mit in dem Alter und Temperatur ein Einklang gebracht, so muss ich die 20% Unsicherheit zumindest diskutieren. Und diese Diskussion, auch wenn sie Spekulativer Natur ist und man sie nicht mit Datensätzen unterfüttern kann muss zumindest Qualitativ dabei sein, um das Potential für größere Schwankungen auszuschließen. Und das hat mir ein Stück weit gefehlt.
Kennen sie das Belgien Paradox. Im Zusammenhang mit https://howbad.info/ hat der Betreiber der Seite der Vermutung aufgestellt, dass Chargen, die, da in Belgien der Hauptherstellungsort für BiontechPfizer ist, Belgien auch die „frischesten“ Lose bekam, und das mit ablaufender Halbarkeit die mRNA zerfällt also die Fähigkeit Schaden anzurichten durch Spike Proteine sinkt. Dies auf Deutschland übertragen, in den westlichen Bundesländern gab es regen Zuspruch für die Impfung entsprechend wurde Zeitnah bei Anlieferung verimpft, im Osten Sachsen Thüringen herrscht eher Zurückhaltung bei der Impfung entsprechend kann da auch das ein oder andere Loss eher Richtung Halbarkeits Ende noch mal zur Verimpfung gekommen sein. Ergo würden Fälle von Sterblichkeit aufgrund dieser Vermutung er dort öfter vorkommen wo die frischesten Lose verimpft wurden. Es ist meiner Ansicht nach nicht auszuschließen, das auch dieser Aspekte die Verteilung von Übersterblichkeit in bestimmten Bundesländern miterklären könnte.
Ohne die Erwähnung von solchen Zusammenhängen, kann man aber wenig neue Daten einfordern, die es ggf. gibt über die Verteilung der Chargen auf Deutschland und deren zeitliche Abgabe an Impflinge. Die Spekulation macht Räume, und sollte nur weil man sie nicht direkt belegen kann nicht erwähnt werden. Das war so ein wenig der Punkt der mir fehlt. Klar ist es greifbarer über Fakten zu reden die Quantitativ vorliegen. Aber diese entziehen sich der Gesamtbetrachtung wenn andere Daten fehlen. Insoweit hätte eine Aufführung von „Da gäbe es übrigens noch weitaus mehr“, mich glücklich gemacht.
LikeLike
Könnte das nachfolgende dazu beitragen, dass wir so gut wie kaum einen Effekt finden?
1.) Der Mensch ist sterblich. Je äter desto sterblicher. Je kränker desto sterblicher. Je kälter desto erkältbarer desto sterblicher. Je mehr Viren oder Impfung umso kränklicher und umso sterblicher. Facit: Impfung = Virus. Sie schützt nicht nur, hat auch hohe Nebenwirkungen, v.a. die RNA Impfung, da der eigentliche Impfstoff erst vom Körper erzeugt wird wie beim Infekt. Folglich: Bei jung bis gealtert und gesund mit Covid oder Impfung = Null Unterschied. Bsp. Die Wuhanverstorbenen hatte in 99.1% (!) eine bekannte Vorerkrankung.
2.) Variabilität der Impfwirkung. RNA ist instabil. Je mehr Fragmente ums wo weniger Wirkstoff und um so mehr Nebenwirkungen kurzfristig bis zu Jahrzehnten und ev. bis in die nächste Generation (wir wissen es nicht): Impfstoff ungleich Impfstoff. Bsp. Medizingeschichte der RNA-Medikamente.
3.) Effektstärke bei Pocken: 1-2 Tote / 1’000’000 Geimpfte (nur 1 Impfung im Leben notwendig) zu 300’000 Tote / 1’000’000 Angesteckte : Effekt 150’000 bis 300’000x. Bei Covid ? (50-100?) Tote / 1’000’000 Geimpfte zu 6’500 Tote / 1’000’000 Infizierte. Effekt 65 -130x. Folglich sehr kleiner, möglicher Spielraum einer Effektstärke.
LikeLike
Nachtrag: 4.) Die Wirkungsdauer der Impfung: 3 Monate. Also ein Tropfen auf den heissen Stein.
LikeLike
Sehr geehrter Herr Wiethölter,
Danke für Ihren sehr interessanten Beitrag. Ich hätte dazu eine technische Frage. (Entschuldigen Sie bitte, falls ich die Erklärung dazu schlicht überlesen haben sollte.) Mir wurde nicht ganz klar, wie Sie für saisonale Trends in den Sterbezahlen korrigieren, und zwar, inwieweit Sie eine multiplikative oder eine additive Korrektur vornehmen. Der saisonale Trend sollte meines Erachtens multiplakativ sein (etwa nach dem Vorbild eines Arrheniusfaktors). Eine solche multiplikative Normierung würde dann idealerweise bei Abwesenheit von Zusatzeffekten auf eine saisonal konstante Sterberate für 2021 führen. Und die prozentualen Abweichungen davon müssten dann spezielle Ursachen haben. Für die Impfungen könnten eine mögliche Schutzwirkung (die nur auf den Anteil schwerer Covidfälle anzuwenden wäre) und mögliche tödliche Nebenwirkungen (die unter Vernachlässigung spezieller Alterseffekte prozentual auf die Gesamtsterberate durchschlüge) solche sein. In erster Näherung (und unter Vernachlässigung der je eigenen Verzögerungseffekte beider mutmaßlicher Wirkungen) würde man aber vielleicht erst einmal einfach die prozentualen Abweichungen von der nach der Normierung erwarteten konstanten Sterberate direkt mit der Impfrate korrelieren. Entspricht das in etwa Ihrem Vorgehen?
LikeLike
Sehr geehrter Herr Kroy,
Danke für Ihren Kommentar. Die meisten der dargestellten Daten sind jeweils kumulative Daten der Bundesländer. Der differenzierende Faktor besteht also im jeweiligen Bundesland selbst. In diesen Darstellungen ist eine saisonale Korrektur nicht notwendig, da der saisonale Einfluss als solcher ein gemeinsamer Faktor aller Bundesländer ist. Eine Korrektur müsste hier dann vorgenommen werden, wenn entweder die Coronawellen und/oder die Saisons sich zeitlich in den einzelnen Bundesländern gravierend voneinander unterscheiden würden, was aber nicht der Fall ist.
Anders ist es in der Zeitreihenbetrachtung der Sterbefälle. Hier ist der saisonale Faktor ein bedeutender. Die saisonale Korrektur geschieht ganz einfach dadurch, dass nicht etwa absolute Zahlen betrachtet werden, sondern die jeweiligen absoluten Abweichungen im betrachteten Jahr von den Zahlen der vergangenen Jahre zu denselben Zeitpunkten (Wochen). Es wird also immer eine jeweilige Woche mit der gleichen Woche der vergangenen Jahre (bzw. des Durchschnitts) verglichen, und zwar unter Berücksichtigung der jeweiligen demografischen Zusammensetzung der Bevölkerung. Ein saisonaler Effekt zu unterschiedlichen Zeiten des Jahres 2021 wird also genauso für die vergangenen Jahre angenommen.
Wenn man so will, ist das dann eine additive (oder auch subtraktive) Betrachtungsweise bzw. eine reine Differenzrechnung, aber keine multiplikative Berechnung. Bei der im Beitrag vorgenommenen Betrachtung müsste nach Eliminierung aller sonstiger Einflussfaktoren ebenfalls eine Abweichungslinie entstehen, die sich um Null bewegt. Theoretisch! Praktisch ist es natürlich nicht möglich, alle möglichen sonstigen Einflussfaktoren präzise zu isolieren. Daher hier auch keine prozentuale Abweichungsberechnung. Die natürlichen wöchentlichen Schwankungen, die nicht durch irgendwelche Faktoren zu erklären sind oder auch ganz einfach zufällig sein können, sind dann doch zu groß, um sie sinnvoll prozentuieren zu können. Es bestünde die Gefahr, dass Aussagen mathematisch generiert und hochdimensioniert würden, die so gar nicht begründet sind.
Eine multiplikative Methode wäre hier auch generell nicht ohne Weiteres anwendbar, da dazu isoliert die Effektstärke von Temperaturen oder auch der jeweiligen Saison bekannt sein müsste oder zumindest die Daten eine solche Berechnung zulassen müssten. Das ist aber nicht der Fall.
Im Fall der Korrelationsberechnung mit mehreren bestimmenden Variablen (z. B. Covid-Tote in Bezug auf Alter und Temperatur) würde sich eine multiplikative Methode durchaus anbieten. Aber auch hier erlauben weder die verfügbaren Daten noch die Herangehensweise eine multiplikative Methode. Die vorgenommene Normierung der Daten auf eine Skala von 0 bis 1 erlaubt in diesem Fall für sich alleine genommen schon keine multiplikative Methode, da Null in diesem Fall nicht ″Nichts“ ist. Der Wert Null stellt den geringsten und 1 den höchsten Wert in den Bundesländern dar. Der Wert Null hat daher nicht nur numerische Qualität (im direkten Vergleich mit den anderen Werten), sondern repräsentiert vor allem auch einen Rang. Die Kombination der Variablen kann ich daher diesem Fall nur additiv vornehmen. Das hat den Nachteil, dass ich dadurch nicht sagen kann, in welcher Stärke welche Variable einen Einfluss haben kann oder auch, welche Einflussstärke die Summe der Variablen haben kann. Ich kann damit nur darstellen, DASS eine Korrelation vorliegt und ich kann darstellen, dass eine bestimmte Betrachtung stärker korreliert als eine andere (oder eben auch nicht). Aber mehr ist damit hier nicht möglich. Es war in diesem Beitrag allerdings auch nicht mein Ziel zu berechnen, wie stark der Effekt der einzelnen Variablen genau sein kann.
Multiplikative Methoden könnten hier zwar weiter führen, aber die verfügbaren Daten sind dieser Form dafür nicht geeignet. Hier müsste eine andere Herangehensweise gewählt werden.
Der Arrheniusfaktor hat meiner Interpretation nach einen eher exponentiellen Charakter (vereinfacht und überhaupt nicht fachmännisch gesagt). Sie haben sicherlich recht, wenn Sie davon ausgehen, dass ein Zusammenhang von Temperaturen (oder in größerem Zusammenhang: Saisons) und Krankheitswellen oder Todesfällen sich nicht unbedingt linear äußert, sondern (zum Teil) exponentiell sein kann. Aber die verwendeten Daten eignen sich nicht dafür, das genauer herauszuarbeiten. Im Sinne meines Beitrags wäre es zwar sicherlich nützlich, dies tun zu können (wenn es möglich wäre), andererseits ist es nicht unbedingt notwendig.
Sie erwähnen mögliche positive aber gleichermaßen auch mögliche negative Effekte der Impfungen. Ich wünschte, ich könnte das genauer untersuchen. Aber es fängt schon damit – schlecht – an, dass bezüglich der Impfungen in Deutschland noch nicht einmal Grund- oder Rohdaten zu ausreichend differenzierten Altersgruppen im Zeitablauf in den Bundesländern verfügbar sind. Warum das überhaupt sein kann, bleibt mir ein Rätsel.
Ich hoffe, Ihre Fragestellung korrekt interpretiert zu haben und ausreichend dazu Stellung genommen zu haben. Falls nicht, dann gerne noch einmal nachhaken.
LikeLike
Es muss Impftote gegeben haben. (Siehe Israel-Grafik) (1). Die Medianzeit vom Ansteckung bis zum Tod liegt bei 4-5 Wochen. 2020 ist diese Zeitverschiebung vorhanden und danach nicht mehr. (2) Dann ereignet sich etwas Unmedizinisches. 2x Impfaktionen in eine Welle! Also Impfstoff + Virus im Körper = schwererer Verlauf. (3) Impfstoff + Erkrankung + Alter besser als Virus + Erkrankung + Alter gilt nur für wenige und nur für eine kurze Zeitspanne. (4) Medizingeschichtlich wird ein RNA-Impfstoff erstmals verwendet. Kenntnisse zur Beurteilung der Impftauglichkeit fehlen. Es wird also wild losgeimpft, was auch sehr unmedizinisch ist. N.b.: Der Impfstoff mit bestem Wirkungs-/Nebenwirkungsverhältnis ist der konjugierte, also klassische Impfstoff aus Kuba!
LikeLike
Wenn ich solche Artikel oder die Studie von Herrn Kuhbandner lese kommt mir eigentlich zuerst Herr Lausen in den Sinn.
Für mich als Statistiklaie ist schon die einfache Kurve von destatis ausreichend um zu Fragen warum man hier nicht genauer hinschauen will. Wir haben seit KW 32/33 dauerhaft eine Sterblichkeit über den einfachen Durchschnitt.
https://www.destatis.de/DE/Themen/Querschnitt/Corona/Gesellschaft/bevoelkerung-sterbefaelle.html
Gemeinsam mit den Ausführungen von Ihnen, Kubandner oder Marcel Barz ist eigentlich völlig klar, dass es keine Übersterblichkeit gab die irgendeine Maßnahme gerechtfertigt hat (was auch der laienhafte Blick auf die Intensivbelegungen vom DIVI unterstreichen). Was aber immer noch kaum jemand glaubt.
Aber diese mehr oder weniger leichte Abweichung der Übersterblichkeit seit beginn der Impfung müsste einen Blick auf Krankenregister hervorrufen (Was Lausen ja schon bei der BBK getan hat) um herauszufinden, ob es spezifische zunahmen von Krankheiten gibt, die einen zusammenhang mit der Impfung vermuten lassen könnten oder ob vielleicht an den Maßnahmen an sich liegt oder ob es vielleicht ganz andere zusammnehänge gibt.
Wenn man die letzten zwei Jahre verfolgt hat und gesehen welche unsinnige Studien geführt wurden, um die Narrative irgendwie zu erfüllen, wundert es den (auch) wissenschaftlichen Laien, das es hier keine Ansätze gibt, dem auf den Grund zu gehen. Aber ich finde das wäre auf jeden Fall der nächste Ort wo man schauen müsste.
Öffentlich zugänglich und nur die Rohdaten ist das InEK und die Sterbestatistik von destatis, aber die geht bisher nur bis 2020.
https://www-genesis.destatis.de/genesis/online?sequenz=statistikTabellen&selectionname=23211
LikeLike